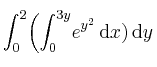Portada del sitio > Fundamentos de Matemáticas > EXÁMENES RESUELTOS > Ingeniería Informática UNED Septiembre 2012 Modelo C
Ingeniería Informática UNED Septiembre 2012 Modelo C
Artículos de esta sección
-
Dada la matrizSolución
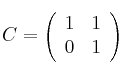 y el conjunto de matrices cuadradas de orden 2:
y el conjunto de matrices cuadradas de orden 2:
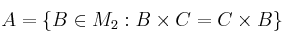 ,
encuentre una base para dicho espacio
,
encuentre una base para dicho espacio -
Dada la matrizSolución
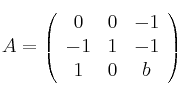 Determine el valor de b para que se cumpla la siguiente igualdad:
Determine el valor de b para que se cumpla la siguiente igualdad:
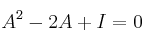 donde
donde 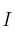 representa la matriz identidad de orden 3.
representa la matriz identidad de orden 3. -
SupongamosSolución
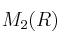 el conjunto de las matrices con coeficientes reales sobre el cuerpo de los números reales, y en él las bases:
el conjunto de las matrices con coeficientes reales sobre el cuerpo de los números reales, y en él las bases:

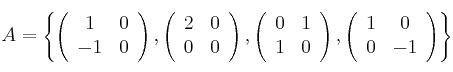

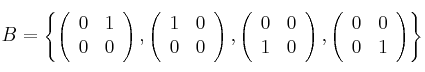 Calcula el determinante de la matriz de cambio de base de la A a la B
Calcula el determinante de la matriz de cambio de base de la A a la B -
Dada la funciónSolución
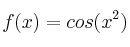 y los nodos
y los nodos 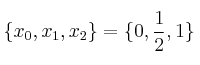 , determine el máximo del polinomio de interpolación de Lagrange de la función en esos nodos, para el intervalo
, determine el máximo del polinomio de interpolación de Lagrange de la función en esos nodos, para el intervalo ![[0,1] [0,1]](local/cache-TeX/ccfcd347d0bf65dc77afe01a3306a96b.png)
-
Supongamos el espacioSolución
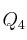 el espacio vectorial generado por los polinomios
el espacio vectorial generado por los polinomios 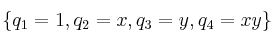 Y consideremos la aplicación
Y consideremos la aplicación 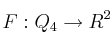 dada por:
dada por:
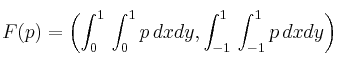 Determine, para la base
Determine, para la base 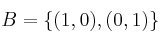 la matriz asociada a
la matriz asociada a 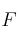
- Solución
- Solución
- Solución
- Solución
- Solución

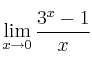
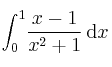
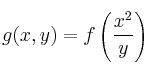 , calcule
, calcule