Portada del sitio > Fundamentos de Matemáticas > EXÁMENES RESUELTOS > Ingeniería Informática UNED Febrero 2011 Modelo C
Ingeniería Informática UNED Febrero 2011 Modelo C
Artículos de esta sección
- Solución
- Solución
- Solución
- Solución
-
Dado el polinomioSolución
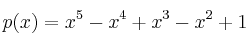 , sabemos que existen coeficientes
, sabemos que existen coeficientes 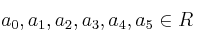 de tal manera que podemos expresar el polinomio en la forma:
de tal manera que podemos expresar el polinomio en la forma:
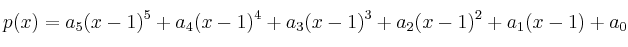 Determine entonces el valor de
Determine entonces el valor de 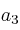
- Solución
- Solución
- Solución
- Solución
-
Suponiendo una funciónSolución
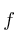 tal que, para los nodos
tal que, para los nodos 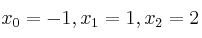 cumple que
cumple que 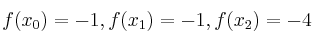 , determine el valor
, determine el valor 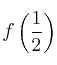 , como aproximación del polinomio de interpolación de Lagrange en dichos nodos
, como aproximación del polinomio de interpolación de Lagrange en dichos nodos

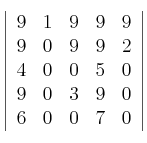
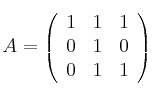 y considerando
y considerando 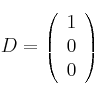 , determine:
, determine:
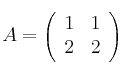 , determine las ecuaciones implícitas del subespacio asociado al valor propio
, determine las ecuaciones implícitas del subespacio asociado al valor propio 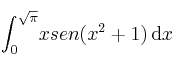
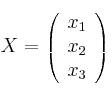 ,
, 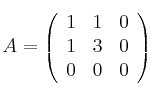 y
y 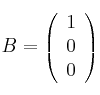 Calcule
Calcule 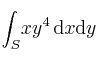 , siendo
, siendo

