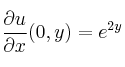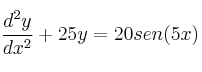Portada del sitio > Fundamentos de Matemáticas > EXÁMENES RESUELTOS > FÍSICA-UNED Ecuaciones Diferenciales Septiembre 2013
FÍSICA-UNED Ecuaciones Diferenciales Septiembre 2013
Artículos de esta sección
-
Dada la ecuación diferencialSolución
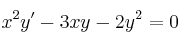 a) Exprésela en la forma
a) Exprésela en la forma 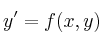 y determine la región del plano donde el teorema de existencia y unicidad garantiza solución única
b) Compruebe que es homogénea y resuélvala
y determine la región del plano donde el teorema de existencia y unicidad garantiza solución única
b) Compruebe que es homogénea y resuélvala - Solución
-
Dada la ecuación diferencialSolución
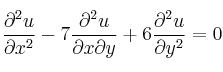 a) Clasifíquela en elíptica, parabólica o hiperbólica
b) Compruebe que
a) Clasifíquela en elíptica, parabólica o hiperbólica
b) Compruebe que 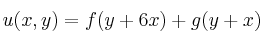 , donde
, donde 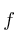 y
y 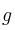 son funciones arbitrarias, es una solución general de la ecuación
c) Encuentre la solución particular que verifique las condiciones de contorno:
son funciones arbitrarias, es una solución general de la ecuación
c) Encuentre la solución particular que verifique las condiciones de contorno:
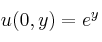 ,
,