Portada del sitio > Fundamentos de Matemáticas > EXÁMENES RESUELTOS > FÍSICA-UNED Álgebra Septiembre 2013 - E
FÍSICA-UNED Álgebra Septiembre 2013 - E
Artículos de esta sección
- Solución
- Solución
-
Dados los planosSolución
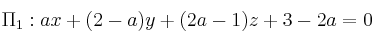
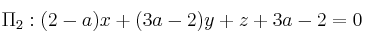 ,
, 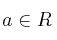 determine los posibles valores de a para que la recta intersección tenga
determine los posibles valores de a para que la recta intersección tenga 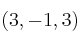 por vector director
por vector director -
Para la aplicación linealSolución
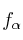 definida de
definida de 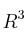 en
en 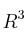 y con matriz asociada
y con matriz asociada
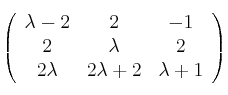 determine una base para el subespacio núcleo y para el subespacio imagen para los valores de
determine una base para el subespacio núcleo y para el subespacio imagen para los valores de 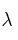 para los que $f_\lambda no es biyectiva
para los que $f_\lambda no es biyectiva -
Para la matrizSolución
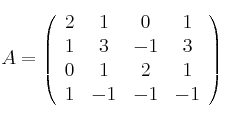 estudie la existencia de una matriz
estudie la existencia de una matriz 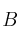 tal que
tal que 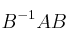 es diagonal y determínla en caso afirmativo
es diagonal y determínla en caso afirmativo