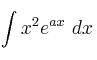Portada del sitio > Fundamentos de Matemáticas > EXÁMENES RESUELTOS > Ingeniería Electr. - Tec. Industrial UNED - Cálculo - Febrero (...)
Ingeniería Electr. - Tec. Industrial UNED - Cálculo - Febrero 2013
Artículos de esta sección
- Solución
- Solución
-
Sabiendo que la funciónSolución
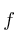 es una función real de variable real tal que
es una función real de variable real tal que 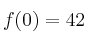 y
y 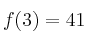 , calcule una aproximación para su integral definida mediante el método del Trapecio
, calcule una aproximación para su integral definida mediante el método del Trapecio -
Dado el puntoSolución
 , expresado en coordenadas cartesianas, determine sus coordenadas esféricas y cilíndricas
, expresado en coordenadas cartesianas, determine sus coordenadas esféricas y cilíndricas - Solución
- Solución

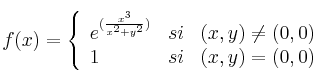 estudie su continuidad y las derivadas parciales
estudie su continuidad y las derivadas parciales