Portada del sitio > Fundamentos de Matemáticas > EXÁMENES RESUELTOS > Ingeniería Informática UNED Febrero 2012 Modelo A
Ingeniería Informática UNED Febrero 2012 Modelo A
Artículos de esta sección
- Solución
- Solución
- Solución
-
Dado el conjuntoSolución
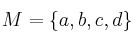 y la Ley de Composición Interna definida por:
y la Ley de Composición Interna definida por: 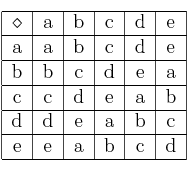 Indique cuál es el inverso del elemento
Indique cuál es el inverso del elemento 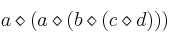
- Solución
- Solución
- Solución
- Solución
- Solución
-
Calcule el valor aproximado y el error que se comete al aproximarSolución
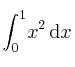 la integral por la Regla de Trapecios, para n=3
la integral por la Regla de Trapecios, para n=3

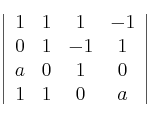 tome valor máximo
tome valor máximo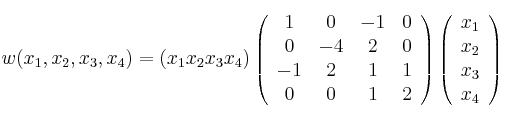 determine las ecuaciones implícitas del subespacio asociado al vector
determine las ecuaciones implícitas del subespacio asociado al vector 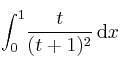
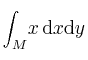 , para el recinto
, para el recinto 
