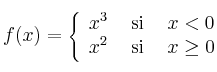Portada del sitio > Fundamentos de Matemáticas > EXÁMENES RESUELTOS > Tecnologías Información UNED Septiembre 2012 Modelo B
Tecnologías Información UNED Septiembre 2012 Modelo B
Artículos de esta sección
- Solución
- Solución
- Solución
- Solución
-
Dada la integral definidaSolución
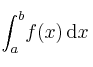 , determine una aproximación de su valor exacto aplicando la fórmula de Simpson
, determine una aproximación de su valor exacto aplicando la fórmula de Simpson -
Dada una matrizSolución
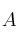 , que hemos introducido en el programa MAXIMA, se ha producido la siguiente salida al escribir la orden
, que hemos introducido en el programa MAXIMA, se ha producido la siguiente salida al escribir la orden 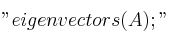 :
:
![[ [ [ -2,4 ] , [ 2,1 ] ] , [ [ [ 1,0,-1 ] , [ 0,1,0 ] ] , [ [ 1,1,0 ] ] ] ] [ [ [ -2,4 ] , [ 2,1 ] ] , [ [ [ 1,0,-1 ] , [ 0,1,0 ] ] , [ [ 1,1,0 ] ] ] ]](local/cache-TeX/d660119704a58b422aa974bae1d57c4e.png) Explique su significado
Explique su significado

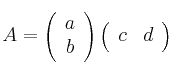
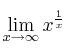
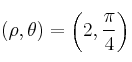 Calcule sus coordenadas cartesianas.
Calcule sus coordenadas cartesianas.