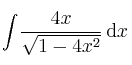Portada del sitio > Fundamentos de Matemáticas > EXÁMENES RESUELTOS > Tecnologías Información UNED Febrero 2012 Modelo B
Tecnologías Información UNED Febrero 2012 Modelo B
Artículos de esta sección
- Solución
- Solución
- Solución
- Solución
- Solución
-
Dado el conjuntoSolución
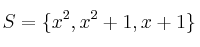 , determine si
, determine si 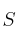 es una base del espacio vectorial de los polinomios de grado menor o igual a 3. En caso de no serlo, determine una base ampliando el conjunto
es una base del espacio vectorial de los polinomios de grado menor o igual a 3. En caso de no serlo, determine una base ampliando el conjunto 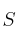
-
Calcule las derivadas parciales de orden 2 de la funciónSolución
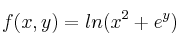 y la matriz Hessiana de la función
y la matriz Hessiana de la función 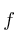 en (0,1)
en (0,1)

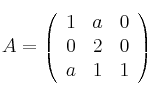 calcule el valor de A para que sea diagonalizable
calcule el valor de A para que sea diagonalizable