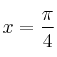
	INICIO Clientes \| Blog MATEMÁTICAS \| QUÍMICA \| FÍSICA \| Matemát. UNIVERSIDAD \| ALEMÁN

Tecnologías Información UNED Febrero 2012 Modelo A

Artículos de esta sección

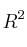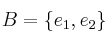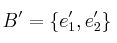Sea el espacio vectorial $R^2$ sobre el cuerpo de los reales y supongamos en él bases $B=\{ e_1,e_2\}$ y $B'=\{e'_1,e'_2\}$ de tal manera que:
$e'_1 = e_1+e_2$
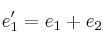
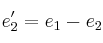$e'_2 = e_1-e_2$ Calcule la matriz asociada al cambio de base de 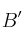$B'$ a $B$
Solución
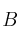
Usando el programa MAXIMA, hemos obtenido el siguiente resultado, para la matriz A y la orden "eigenvectros(A)": $[[[2],[3]],[[[1,2,0],[0,0,1]]]]$ , ¿cuál es la conclusión que se extrae?
Solución
Calcule el valor del siguiente límite: $\displaystyle\lim_{n \to{+}\infty}{\left(\frac{2+n^3}{1+n^3}\right)^{2(n^2+1)}}$
Solución
Define lo que se entiende por gradiente de una función $f:R^3\rightarrow R$ , si existe
Solución
Calcule el valor del área encerrada por la función $f(x)=3ln(x)$ y el eje $X$ , entre los valores $x=1$ y $x=e$
Solución
Sea la aplicación 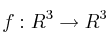$f:R^3\rightarrow R^3$ un endomorfismo tal que:
$f(1,0,0)=(1,0,0)$
$f(0,1,0)=(1,2,0)$
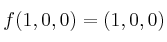
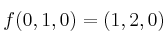
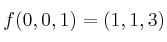$f(0,0,1)=(1,1,3)$ Calcule valores propios y la correspondiente matriz de paso
Solución
Calcule el polinomio de Taylor de orden 3 para la función $f(x)=sen(x)$ en el punto $x=\frac{\pi}{4}$
Solución