Portada del sitio > Fundamentos de Matemáticas > EXÁMENES RESUELTOS > Ingeniería Informática UNED Febrero 2011 Modelo A
Ingeniería Informática UNED Febrero 2011 Modelo A
Artículos de esta sección
-
SeaSolución
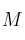 el conjunto de las funciones reales de variable real continuas en todo
el conjunto de las funciones reales de variable real continuas en todo 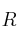 .Definimos el producto:
.Definimos el producto:
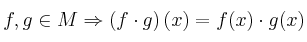 Determine entonces si alguna de las funciones siguientes tiene inversa para dicho producto:
Determine entonces si alguna de las funciones siguientes tiene inversa para dicho producto:

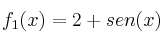

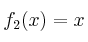

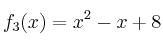

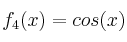
- Solución
-
Dados los espacios vectorialesSolución
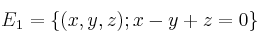 y
y 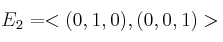 (subespacio generado por los vectores), determine el subespacio intersección de ambos
(subespacio generado por los vectores), determine el subespacio intersección de ambos - Solución
- Solución
- Solución
- Solución
- Solución
- Solución
- Solución

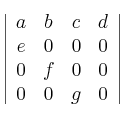
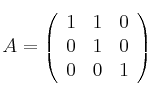 .
Determine una base del subespacio asociado al valor propio
.
Determine una base del subespacio asociado al valor propio 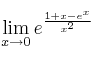
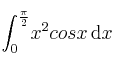
 , siendo
, siendo

