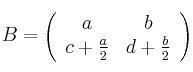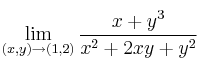Portada del sitio > Fundamentos de Matemáticas > EXÁMENES RESUELTOS > Ingeniería Informática UNED Septiembre 2012 Modelo A
Ingeniería Informática UNED Septiembre 2012 Modelo A
Artículos de esta sección
-
Sea la matrizSolución
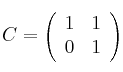 y el conjunto de matrices cuadradas de orden 2x2
y el conjunto de matrices cuadradas de orden 2x2
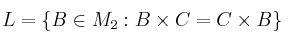 Compruebe si la suma y el producto usuales de matrices son conmutativas en el conjunto L
Compruebe si la suma y el producto usuales de matrices son conmutativas en el conjunto L - Solución
-
Dado el conjuntoSolución
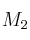 de las matrices cuadradas de orden 2, tomamos la base
de las matrices cuadradas de orden 2, tomamos la base
 y consideramos la aplicación
y consideramos la aplicación  , definida por:
, definida por:







 Calcule entonces:
Calcule entonces:

-
DadoSolución
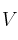 un espacio vectorial de dimensión 2 y, en él las bases
un espacio vectorial de dimensión 2 y, en él las bases 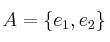 y
y 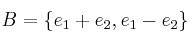 . Sea también
. Sea también 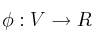 una forma bilineal con matriz asociada respecto de la base A:
una forma bilineal con matriz asociada respecto de la base A:
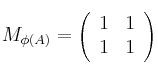 Calcule entonces la matriz asociada a
Calcule entonces la matriz asociada a 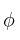 respecto de la base
respecto de la base 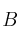
-
Calcule el error exacto que se comete al aproximar la integralSolución
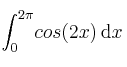 por el método de los trapecios con n=4 y subintervalos de igual longitud
por el método de los trapecios con n=4 y subintervalos de igual longitud - Solución
-
Dada la funciónSolución
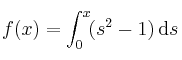 ¿cuál sería el valor de
¿cuál sería el valor de 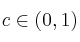 que hace que se verifique el teorema del valor medio del cálculo diferencial en el intervalo
que hace que se verifique el teorema del valor medio del cálculo diferencial en el intervalo ![[0,1] [0,1]](local/cache-TeX/ccfcd347d0bf65dc77afe01a3306a96b.png)
- Solución
- Solución
-
SeaSolución
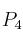 el espacio vectorial generado por los polinomios:
el espacio vectorial generado por los polinomios:
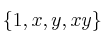 y dentro de
y dentro de 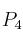 , el conjunto:
, el conjunto:
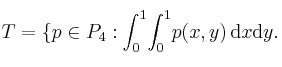 .
Determine las ecuaciones implícitas de dicho subespacio
.
Determine las ecuaciones implícitas de dicho subespacio

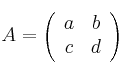 tiene determinante
tiene determinante