Portada del sitio > Fundamentos de Matemáticas > EXÁMENES RESUELTOS > Ingeniería Informática UNED Febrero 2012 Modelo D
Ingeniería Informática UNED Febrero 2012 Modelo D
Artículos de esta sección
- Solución
- Solución
-
Dado el espacio vectorialSolución
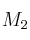 de las matrices de orden 2, determine dos conjuntos que formen una base de dicho espacio
de las matrices de orden 2, determine dos conjuntos que formen una base de dicho espacio -
Consideramos el conjuntoSolución
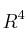 con la Ley de Composición Interna
con la Ley de Composición Interna 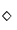 dada por:
dada por:
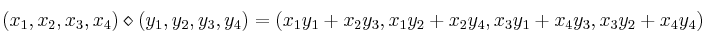 Determine el elemento neutro para dicha operación
Determine el elemento neutro para dicha operación -
Dada la forma bilinealSolución
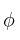 en el cuerpo
en el cuerpo 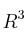 , cuya expresión es:
, cuya expresión es:
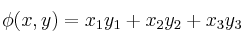 , donde
, donde 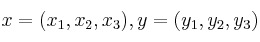 están referidos a la base cacónica de
están referidos a la base cacónica de 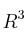 :
:
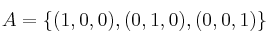 .
¿Cuál sería la matriz asociada a la nueva base
.
¿Cuál sería la matriz asociada a la nueva base 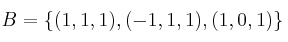 ?
? - Solución
-
Si llamamosSolución
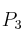 al polinomio de Taylor de orden 3 asociado a la función
al polinomio de Taylor de orden 3 asociado a la función 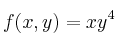 en el punto
en el punto 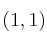 , ¿cuál es el valor de
, ¿cuál es el valor de 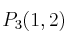 ?
? -
Dada la aplicación T deSolución
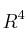 en
en 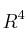 , determinada por la expresión:
, determinada por la expresión:
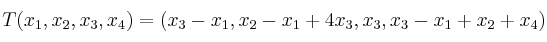 ,
¿cuál es el determinante de su matriz asociada?
,
¿cuál es el determinante de su matriz asociada? - Solución

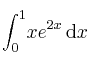
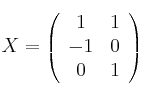 y
y 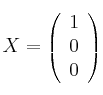 y suponiendo la matriz
y suponiendo la matriz
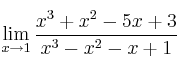
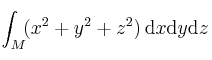 ,
siendo
,
siendo 
