Portada del sitio > Fundamentos de Matemáticas > EXÁMENES RESUELTOS > Tecnologías Información UNED Septiembre 2012 Modelo A
Tecnologías Información UNED Septiembre 2012 Modelo A
Artículos de esta sección
-
Dado el grupoSolución
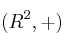 , de los pares de números reales con la suma usual, defina un producto "
, de los pares de números reales con la suma usual, defina un producto "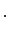 " por elementos del cuerpo
" por elementos del cuerpo 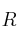 de los números reales de forma que
de los números reales de forma que 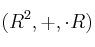 sea un espacio vectorial
sea un espacio vectorial -
SeaSolución
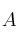 el subespacio de
el subespacio de 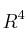 generado por los vectores
generado por los vectores 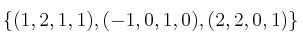 y el subespacio
y el subespacio 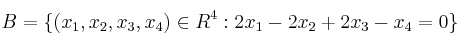 .
Determine entonces las dimensiones de
.
Determine entonces las dimensiones de 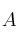 y de
y de 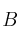
- Solución
-
Dada la funciónSolución
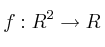 , cuya expresión analítica es:
, cuya expresión analítica es:
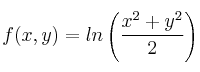 determine el plano tangente a la gráfica de dicha función por el punto
determine el plano tangente a la gráfica de dicha función por el punto 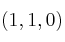
-
Para la función real de variable real, dada por:Solución
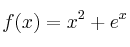 determine el polinomio de Taylor de orden 3 centrado en el origen
determine el polinomio de Taylor de orden 3 centrado en el origen - Solución
- Solución

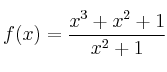 tiene alguna asíntota
tiene alguna asíntota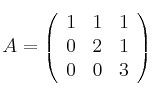 encuentre las ecuaciones de los subespacios propios de A
encuentre las ecuaciones de los subespacios propios de A