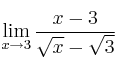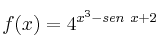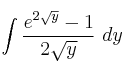
	INICIO Clientes \| Blog MATEMÁTICAS \| QUÍMICA \| FÍSICA \| Matemát. UNIVERSIDAD \| ALEMÁN

Portada del sitio > Fundamentos de Matemáticas > EXÁMENES RESUELTOS > ADE - Matemáticas II - UNED - Septiembre 2012 Modelo A

ADE - Matemáticas II - UNED - Septiembre 2012 Modelo A

Artículos de esta sección

Calcule el límite siguiente: $\lim_{x\rightarrow 3}{\frac{x-3}{\sqrt{x}-\sqrt{3}}}$
Solución
¿Qué se entiende por discontinuidad evitable de una función en un punto?
Calcule la derivada de la función real de variable real $f(x)=4^{x^3-sen\ x+2}$
Solución
¿Cómo se define la derivada de una función real de variable real $f$ en un punto $x_0$ de su dominio?
Calcule una primitiva para: $\int \frac{e^{2\sqrt{y}}-1}{2\sqrt{y}}\ dy$
Solución
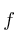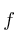Suponiendo una función real $f$ acotada inferiormente por m y superiormente por M en un intervalo $[a,b]\ ,\ a<b$ , ¿cómo se podría acotar la integral de $f$ en ese intervalo?
Solución
¿Cuál es la condición que se debe cumplir necesariamente para que la función de dos variables $f$ tenga un extremo en el punto $(x_0,y_0)$
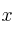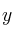La función beneficio obtenida en función de dos recursos $x$ e $y$ viene dada por la expresión: 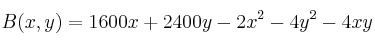$B(x,y)=1600x+2400y-2x^2-4y^2-4xy$ ¿Cuándo es máximo dicho beneficio?
Solución
¿Qué se debe exigir para que una función de dos variables tenga un extremo en un punto?
Encuentre los extremos de la función $f(x,y)=2-3x^2+3x^2y+y^3-3y^2$
Solución