Portada del sitio > Lógica y Estructuras Discretas > EXÁMENES RESUELTOS > UNED - Septiembre 2012 - Modelo A
UNED - Septiembre 2012 - Modelo A
Artículos de esta sección
-
Solución
Para las fórmulas

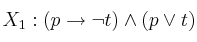

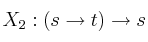

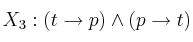

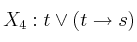
y la interpretación
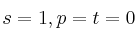 , indique las fórmulas que satisface de entre las siguientes:
, indique las fórmulas que satisface de entre las siguientes: a)
a) 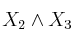
 b)
b) 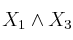
 c)
c) 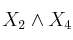
- Solución
- Solución
-
Sean las fórmulas de lógica proposicional cualesquieraSolución
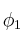 ,
, 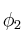 y
y 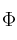 . Indica si alguna de las siguientes afirmaciones es cierta:
. Indica si alguna de las siguientes afirmaciones es cierta:

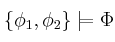 si, y sólo si
si, y sólo si 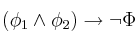 es tautología
es tautología

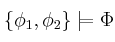 si, y sólo si
si, y sólo si 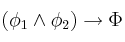 es tautología
es tautología

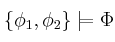 si, y sólo si
si, y sólo si 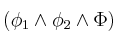 es insatisfacible
es insatisfacible - Solución
- Solución
- Solución
-
Solución
Sea
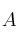 un conjunto cualquiera, y sea E el conjunto universal. Indique si alguna de las siguientes fórmulas es equivalente a
un conjunto cualquiera, y sea E el conjunto universal. Indique si alguna de las siguientes fórmulas es equivalente a 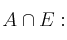
 a)
a) 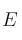
 b)
b) 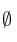
 c)
c) 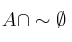
- Solución
- Solución
0 | 10


