Portada del sitio > Lógica y Estructuras Discretas > EXÁMENES RESUELTOS > UNED - Febrero 2012 - Modelo A
UNED - Febrero 2012 - Modelo A
Artículos de esta sección
- Solución
- Solución
- Solución
- Solución
-
Solución
Indique, sabiendo que
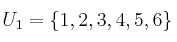
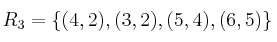
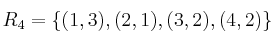 ,
,la afirmación correcta, para
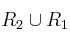 :
: a) es función no inyectiva de
a) es función no inyectiva de 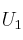 en
en 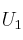
 b) no es función de
b) no es función de 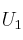 en
en 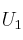
 c) es función sobreyectiva de
c) es función sobreyectiva de 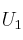 en
en 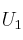
 d) es función biyectiva de
d) es función biyectiva de 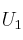 en
en 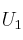
-
Solución
Indique, sabiendo que
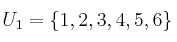
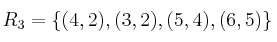
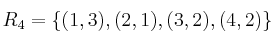 ,
,la afirmación correcta, para
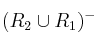 :
: a) es función no inyectiva de
a) es función no inyectiva de 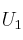 en
en 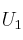
 b) no es función de
b) no es función de 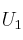 en
en 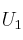
 c) es función sobreyectiva de
c) es función sobreyectiva de 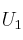 en
en 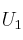
 d) es función biyectiva de
d) es función biyectiva de 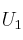 en
en 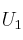
- Solución
- Solución
- Solución
-
Solución
Siendo las fórmulas:
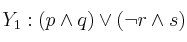
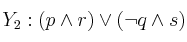
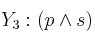
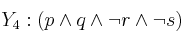 Completa la frase siguiente con uno de los cuatro apartados entre paréntesis separados por comas:
Completa la frase siguiente con uno de los cuatro apartados entre paréntesis separados por comas:
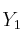 es consecuencia de .....................
es consecuencia de .....................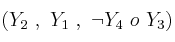
0 | 10


