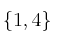Portada del sitio > Lógica y Estructuras Discretas > EXÁMENES RESUELTOS > UNED - Febrero 2012 - Modelo C
UNED - Febrero 2012 - Modelo C
Artículos de esta sección
-
Solución
Dados los conjuntos
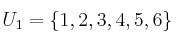
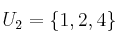
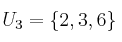
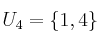
indica las afirmaciones verdaderas o falsas de las siguientes:
 a)
a) 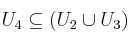
 b)
b) 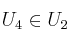
 c)
c) 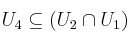
 d) El conjunto potencia de
d) El conjunto potencia de 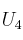 tiene cuatro elementos
tiene cuatro elementos - Solución
-
Solución
Dadas:
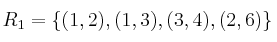
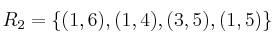
indique si, para
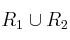 verifica alguna de las afirmaciones siguientes:
verifica alguna de las afirmaciones siguientes: a) es una relación de equivalencia
a) es una relación de equivalencia
 b) es una relación simétrica
b) es una relación simétrica
 c) es una relación de orden total
c) es una relación de orden total
 d) es una relación de orden parcial estricto
d) es una relación de orden parcial estricto -
Solución
Siendo
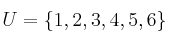
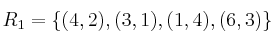
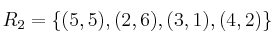
indique, para
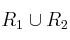 si las siguietes afirmaciones son correctas o falsas:
si las siguietes afirmaciones son correctas o falsas: a) es una función no inyectiva de
a) es una función no inyectiva de 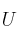 en
en 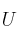
 b) es biyectiva
b) es biyectiva
 c) es sobreyectiva
c) es sobreyectiva
 d) su inversa es función de
d) su inversa es función de 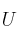 en
en 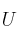
- Solución
-
Dada la fórmulaSolución
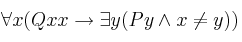 sobre el universo
sobre el universo 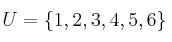 y
y 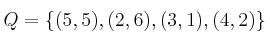 , indique si es falsa o verdadera en el caso de que represente a P:
a)
, indique si es falsa o verdadera en el caso de que represente a P:
a) 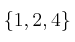 b)
b) 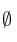 c)
c) 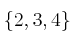 d)
d)