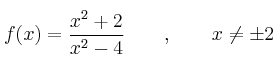Portada del sitio > MAT - 2º BACHILLERATO > Integrales II - Métodos de Integración
Integrales II - Métodos de Integración
Ejercicios de Ampliación
Artículos de esta sección
-
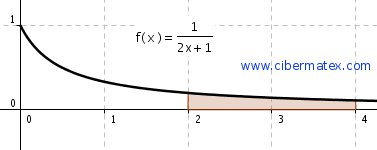
Se considera la función real de variable real definida por:
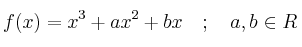 .
. a) ¿Qué valores deben tomar
a) ¿Qué valores deben tomar 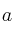 y
y 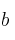 para que
para que 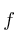 tenga un máximo relativo en el punto
tenga un máximo relativo en el punto 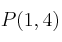 ?
?
 b) Para
b) Para 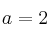 ,
, 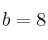 , determínense los puntos de corte de la gráfica de
, determínense los puntos de corte de la gráfica de 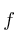 con los ejes de coordenadas y determínense los puntos de inflexión de dicha gráfica.
con los ejes de coordenadas y determínense los puntos de inflexión de dicha gráfica.
 c) Para
c) Para 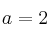 ,
, 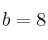 , calcúlese el área del recinto plano acotado limitado por la gráfica de
, calcúlese el área del recinto plano acotado limitado por la gráfica de 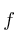 y el eje
y el eje 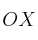 .
.

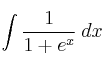
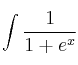
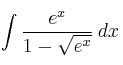
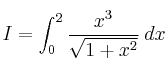
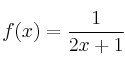 , cuando
, cuando