
	INICIO Clientes \| Blog MATEMÁTICAS \| QUÍMICA \| FÍSICA \| Matemát. UNIVERSIDAD \| ALEMÁN

14-Geometría en el plano

Todos los Ejercicios del Tema

Artículos de esta sección

Halla las ecuaciones vectorial, paramétricas, continua y general de la siguiente recta:
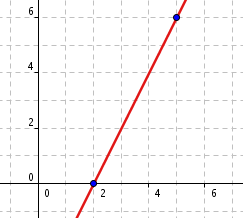
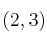
Halla la ecuación explícita de la recta que pasa por el punto $(2,3)$ y tiene como vector director $\vec{v}(1,4)$
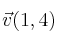
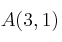
Halla las ecuaciones vectorial, paramétricas, continua, general y explícita de la recta que pasa por los puntos $A(3,1)$ y $B(5,7)$
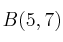
Halla la pendiente, por varios métodos, de la siguiente recta:
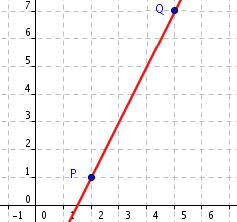
Halla la posición relativa de las rectas:
$r \rightarrow -x+3y+4=0$ $s \rightarrow 3x-9y-12=0$
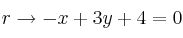
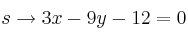
Halla la posición relativa de las rectas:
$r \rightarrow 5x+y+3=0$ $s \rightarrow x-2y+16=0$
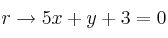
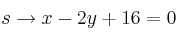
Halla el ángulo que forman las rectas:
$r \equiv \left\{ \begin{array}{ll} x = 3-2t \\ y = 7+t \end{array} \right.$
$s \equiv \left\{ \begin{array}{ll} x = 1-4t \\ y = 4+3t \end{array} \right.$
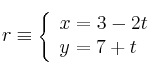
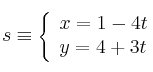
Dadas las rectas:
$R_1 \equiv \left\{ \begin{array}{ll} x = 3-2t \\ y = 7+t \end{array} \right.$
$R_2 \equiv \left\{ \begin{array}{ll} x = 1-4t \\ y = 4+3t \end{array} \right.$
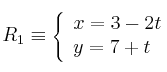
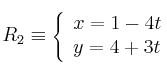
Se pide:

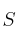
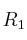
una recta $S$ paralela a $R_1$ por el punto $(5,7)$
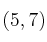
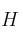
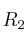
una perpendicular $H$ , a $R_2$ por el punto $(0,0)$
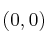
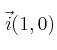
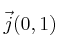
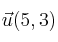
Demuestras que los vectores $\vec{i}(1,0)$ y $\vec{j}(0,1)$ forman una base ortonormal y expresa el vector $\vec{u}(5,3)$ respecto de dicha base.
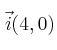
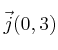
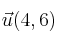
Demuestra que los vectores $\vec{i} (4,0)$ y $\vec{j}(0,3)$ forman una base ortogonal. Expresa el vector $\vec{u} (4,6)$ en función de dicha base.