Cálculo Diferencial en varias variables
Todos los Ejercicios del Tema
Artículos de esta sección
-
Dadas las funciones
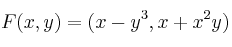
y
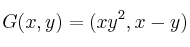
, calcule la matriz jacobiana de
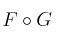
en (1,1)
-
-
Calcule el límite:
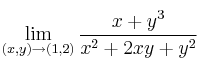
-
Dada la función
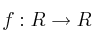
con derivada continua y, a partir de ella, la función
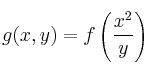
, calcule
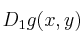
y
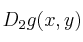
-
Calcule las derivadas parciales de orden 2 de la función 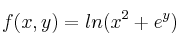 y la matriz Hessiana de la función
y la matriz Hessiana de la función 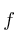 en (0,1)
en (0,1)
Solución
-
Dada la función 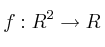 , cuya expresión analítica es:
, cuya expresión analítica es:
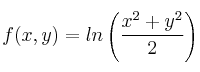 determine el plano tangente a la gráfica de dicha función por el punto
determine el plano tangente a la gráfica de dicha función por el punto 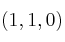
Solución
-
Encuentre los puntos críticos de la función 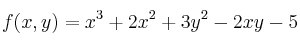
-
Si consideramos 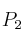 el polinomio de Taylor de orden dos de la función
el polinomio de Taylor de orden dos de la función 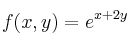 , calcule
, calcule 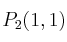
-
-
Determine las dimensiones de un paralelepípedo rectangular cuyo volumen es de 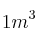 de tal manera que su área sea mínima ¿Y para que sea máxima?
de tal manera que su área sea mínima ¿Y para que sea máxima?
YouTube Twitter

