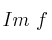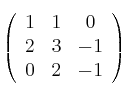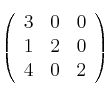Portada del sitio > Fundamentos de Matemáticas > Aplicaciones Lineales y Matrices
Aplicaciones Lineales y Matrices
Todos los Ejercicios del Tema
Artículos de esta sección
- Solución
-
Para la aplicación linealSolución
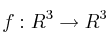 con matriz asociada
con matriz asociada
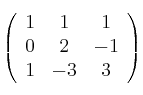 calcule cuál sería la columna primera correspondiente a la matriz asociada a la base
calcule cuál sería la columna primera correspondiente a la matriz asociada a la base 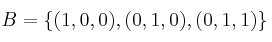
- Solución
- Solución
- Solución
-
Indique si la aplicación definida entre los espacios vectoriales de las matrices cuadradas de orden dos y los polinomios de grado menor o igual que dos, que viene determinada por la expresión:Solución
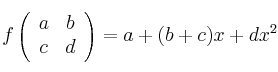 es lineal
es lineal -
En una matrizSolución
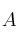 cuadrada de orden 3, cuyas filas suman 1, determine un vector propio asociado al valor propio
cuadrada de orden 3, cuyas filas suman 1, determine un vector propio asociado al valor propio 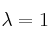
-
Se define la traza de una matrizSolución
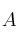 cuadrada de orden
cuadrada de orden 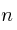 (
(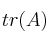 ), como la suma de los elementos de la diagonal principal de dicha matriz. Compruebe si es cierto, para dos matrices
), como la suma de los elementos de la diagonal principal de dicha matriz. Compruebe si es cierto, para dos matrices 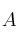 y
y 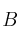 cuadradas de orden
cuadradas de orden 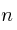 :
:
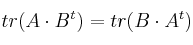
-
Dada la aplicación linealSolución
![f:R_2[x]\rightarrow R_3[x] f:R_2[x]\rightarrow R_3[x]](local/cache-TeX/85dc57b7b577fa6a1f3478db60c2dbb6.png) cuya expresión es
cuya expresión es 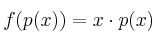 , encuentre la matriz asociada para bases respectivas
, encuentre la matriz asociada para bases respectivas 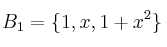 y
y 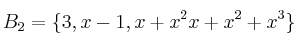 e indique también una base para el subespacio
e indique también una base para el subespacio