No es válida porque estás cayendo en el principal error de este tipo de ejercicios: "el producto de matrices no es conmutativo".
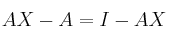
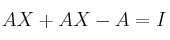
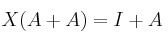 (aquí está el error)
(aquí está el error)
La matriz A está multiplicando por la izquierda, por tanto lo correcto sería:
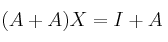
A partir de ahí puedes usar el razonamiento del vídeo (poner 2A y pasar el 2 dividiendo) o también ese válido el razonamiento tuyo: hacer la inversa de A+A (pero multiplicando por la izquierda)