ECUACIONES DIFERENCIALES
Ejercicios de Ampliación
Artículos de esta sección
-
Resuelva la siguiente ecuación diferencial:
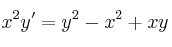
-
Determine la ecuación diferencial de la familia de rectas que pasen por un punto 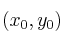 , donde
, donde 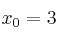 y donde
y donde 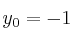
Determine las curvas trayectorias ortogonales a la familia anterior$.
Extraiga conclusiones para las gráficas de ambas familias
-
-
¿Cuál es la solución del sistema de ecuaciones diferenciales
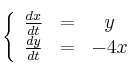
-
Resuelva la ecuación diferencial
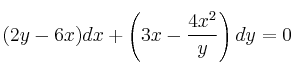
¿Es exacta?
-
Para la ecuación diferencial siguiente, encuentre su solución general, para lo que se necesitarán soluciones linealmente independientes y Wronskiano:
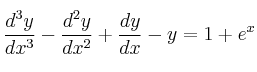
-
Suponiendo
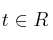
, encuentre una matriz fundamental para el sistema
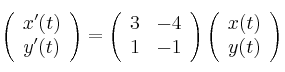
Compruebe sus propiedades y encuentre también una solución particular
YouTube Twitter

