Cálculo Diferencial en varias variables
Ejercicios de Ampliación
Artículos de esta sección
-
Calcule el límite siguiente:
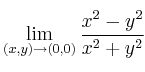
-
Determine la derivada direccional
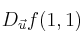
, para la función
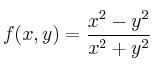
y el vector
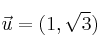
-
Para la función
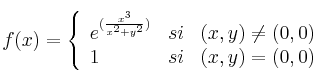
estudie su continuidad y las derivadas parciales
-
Encuentre los extremos de la función
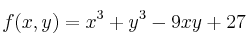
-
La función beneficio obtenida en función de dos recursos
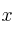
e
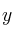
viene dada por la expresión:
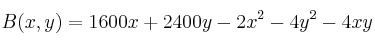
¿Cuándo es máximo dicho beneficio?
-
Encuentre los extremos de la función
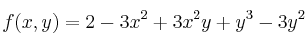
-
¿Cuál sería la derivada direccional de la función
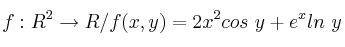
?
-
Calcule la diferencial de la función real de variable vectorial
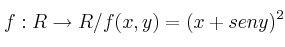
-
Para la función a trozos dada por la expresión
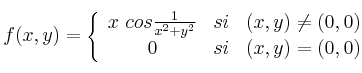
estudie su continuidad y diferenciabilidad
-
Calcule la diferencial de la función
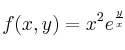
YouTube Twitter

