
	INICIO Clientes \| Blog MATEMÁTICAS \| QUÍMICA \| FÍSICA \| Matemát. UNIVERSIDAD \| ALEMÁN

Portada del sitio > Fundamentos de Matemáticas > Aplicaciones Lineales y Matrices

Aplicaciones Lineales y Matrices

Ejercicios de Ampliación

Artículos de esta sección

Dado el conjunto $M_2$ de las matrices cuadradas de orden 2, tomamos la base $B=\{v_1=\left( \begin{array}{cc} 0 & 0 \\ 0 & -1 \end{array} \right), v_2=\left( \begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array} \right), v_3=\left( \begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array} \right), v_4=\left( \begin{array}{cc} 0 & 0 \\ 1 & 0 \end{array} \right)\}$ y consideramos la aplicación $f:M_2\rightarrow M_2$ , definida por:
$f(v_1)=v_1+v_2+v_3-v_4$
$f(v_2)=v_1+v_2-v_3$
$f(v_3)=-2v_2$
$f(v_4)=-v_2+4v_3$ Calcule entonces: $f(\left( \begin{array}{cc} 0 & -1 \\ 1 & -1 \end{array} \right))$
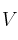
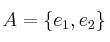
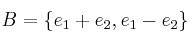
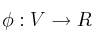
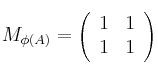
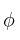
Dado $V$ un espacio vectorial de dimensión 2 y, en él las bases $A=\{ e_1, e_2\}$ y $B=\{ e_1+e_2,e_1-e_2\}$ . Sea también $\phi :V\rightarrow R$ una forma bilineal con matriz asociada respecto de la base A: $M_{\phi(A)}=\left( \begin{array}{cc} 1 & 1 \\ 1 & 1 \end{array} \right)$ Calcule entonces la matriz asociada a $\phi$ respecto de la base $B$
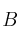
Usando el programa MAXIMA, hemos obtenido el siguiente resultado, para la matriz A y la orden "eigenvectros(A)": $[[[2],[3]],[[[1,2,0],[0,0,1]]]]$ , ¿cuál es la conclusión que se extrae?
Sea la aplicación $f:R^3\rightarrow R^3$ un endomorfismo tal que:
$f(1,0,0)=(1,0,0)$
$f(0,1,0)=(1,2,0)$
$f(0,0,1)=(1,1,3)$ Calcule valores propios y la correspondiente matriz de paso
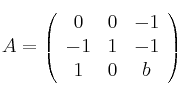
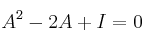
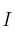
Dada la matriz $A=\left( \begin{array}{ccc} 0 & 0 & -1 \\ -1 & 1 & -1 \\ 1 & 0 & b \end{array} \right)$ Determine el valor de b para que se cumpla la siguiente igualdad: $A^2-2A+I=0$ donde $I$ representa la matriz identidad de orden 3.
Supongamos $M_2(R)$ el conjunto de las matrices con coeficientes reales sobre el cuerpo de los números reales, y en él las bases:
$A=\left\{ \left( \begin{array}{cc} 1 & 0 \\ -1 & 0 \end{array} \right) , \left( \begin{array}{cc} 2 & 0 \\ 0 & 0 \end{array} \right) , \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right) , \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right) \right\}$
$B=\left\{\left( \begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array} \right) , \left( \begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array} \right) , \left( \begin{array}{cc} 0 & 0 \\ 1 & 0 \end{array} \right) , \left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \end{array} \right) \right\}$ Calcula el determinante de la matriz de cambio de base de la A a la B
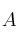
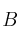
Indique si es cierta la siguiente igualdad, para $A$ y $B$ matrices cuadradas de orden nxn: $det(A+B)=det(A)+det(B)$
Determine la matriz inversa de las siguientes:
$A=\left( \begin{array}{cc} 1 & 2 \\ 0 & 1 \end{array} \right)$
$B=\left( \begin{array}{ccc} 3 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right)$
$C=\left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{array} \right)$
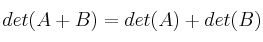
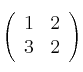
Dada la matriz $\left(\begin{array}{cc}1&2\\3&2\end{array}\right)$ , encuentre sus valores propios e indique si es diagonalizable
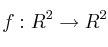
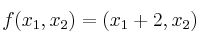
Dada la función $f:R^2\rightarrow R^2$ , dada por $f(x_1,x_2)=(x_1+2,x_2)$ , determine si es o no lineal