Portada del sitio > Lógica y Estructuras Discretas > 3 - Conjuntos, relaciones y funciones
3 - Conjuntos, relaciones y funciones
Ejercicios de Ampliación
Artículos de esta sección
-
Entre los conjuntos
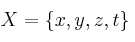 e
e 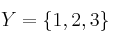 establecemos la siguiente relación:
establecemos la siguiente relación: 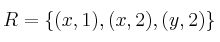 . Calcule:
. Calcule:
 a) el dominio y rango de
a) el dominio y rango de 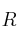
 b) el cardinal de
b) el cardinal de 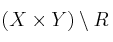
 c) el cardinal de la relación inversa
c) el cardinal de la relación inversa
 d) el cardinal de la relación complementaria
d) el cardinal de la relación complementaria
0 | 10


