10-Sistemas de Ecuaciones
Todos los Ejercicios del Tema
Artículos de esta sección
-
Resuelve el sistema de ecuaciones:
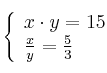
-
Resuelve el sistema de ecuaciones:
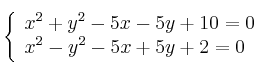
-
Resuelve el sistema de ecuaciones:
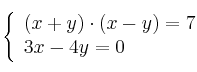
-
Resuelve por el método de Gauss el sistema de ecuaciones:
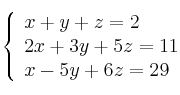
-
Resuelve por el método de Gauss el sistema de ecuaciones:
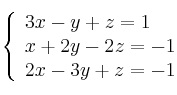
-
Resuelve el sistema de ecuaciones:
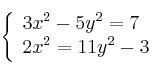
-
Resuelve el sistema de ecuaciones:
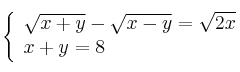
-
Resuelve el sistema de ecuaciones:
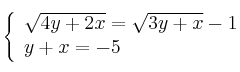
-
Resuelve el sistema de ecuaciones:
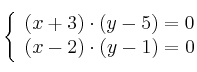
-
Resuelve el sistema de ecuaciones:
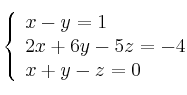
YouTube Twitter

