14-Geometría en el plano
Todos los Ejercicios del Tema
Artículos de esta sección
-
Halla dos puntos y el vector director de la recta
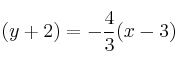
-
Halla dos puntos y el vector director de la recta
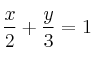
-
-
Halla las coordenadas del punto
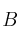
, siendo
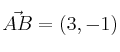
y
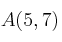
-
Dados los puntos
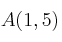
,
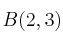
,
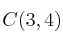
y
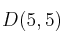
averigua si son equipolentes los vectores
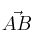
y
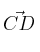
-
Representa gráficamente el vector
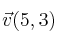
sabiendo que tiene su origen en
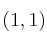
. Averigua punto final y módulo de dicho vector.
-
Averigua si los puntos
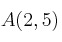
,
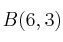
,

y
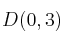
pueden ser los vértices de un paralelogramo.
-
Dados los puntos
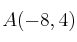
y
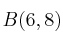
, halla la ecuación de la recta que pasa por el punto medio del segmento
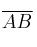
y es paralela a la recta
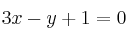
.
-
Dados los puntos
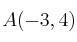
y
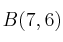
, halla la ecuación de la recta que pasa por el punto medio del segmento
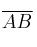
y es perpendicular a la recta
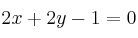
.
-
YouTube Twitter

