14-Geometría en el plano
Todos los Ejercicios del Tema
Artículos de esta sección
-
Los vértices consecutivos de un paralelogramo son
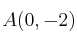
,
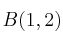
,
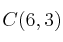
y
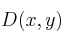
. Halla las coordenadas del vértice D.
-
Los vértices consecutivos de un paralelogramo son
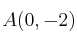
,
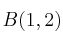
,
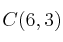
y
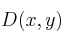
. Halla las coordenadas del vértice D.
-
Dados los vectores
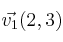
,
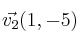
,
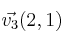

Investiga si
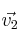
y
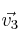
forman una base

Expresa
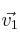
como combinación lineal de
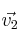
y
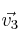
-
Expresa el vector
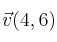
en combinación lineal de los vectores
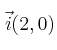
y
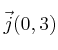
de dos formas: gráfica y analíticamente
-
Halla las ecuaciones
vectorial,
paramétrica y
continua de las rectas:

Pasa por el punto
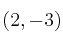
y su vector director es
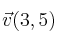

Pasa por el punto
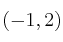
y su vector director es
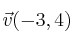
-
Halla dos puntos y el vector director de la recta
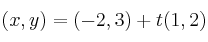
-
Halla dos puntos y el vector director de la recta
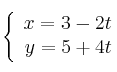
-
Halla dos puntos y el vector director de la recta
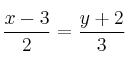
-
Halla dos puntos y el vector director de la recta
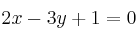
-
Halla dos puntos y el vector director de la recta
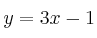
YouTube Twitter

