Cálculo Integral con una variable
Todos los Ejercicios del Tema
Artículos de esta sección
-
Resuelve la integral:

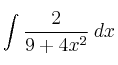
-
Calcule el valor de la integral:
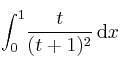
-
Calcula el valor de la integral definida:
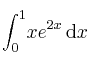
-
Dada la función
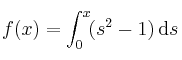
¿cuál sería el valor de
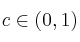
que hace que se verifique el teorema del valor medio del cálculo diferencial en el intervalo
![[0,1] [0,1]](local/cache-TeX/ccfcd347d0bf65dc77afe01a3306a96b.png)
-
Calcule el valor del área encerrada por la función
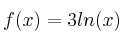
y el eje
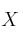
, entre los valores
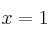
y
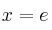
-
Calcula el valor de la integral:
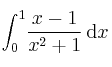
-
Calcule:
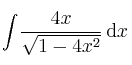
-
Calcule el valor de la integral:
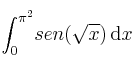
Ayuda: Puede hacer el cambio 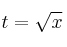
Solución
-
Calcule la integral:
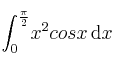
-
Calcule el valor de la integral:
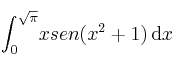
YouTube Twitter

