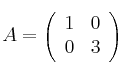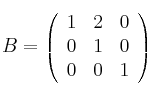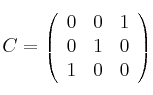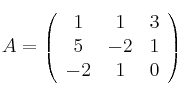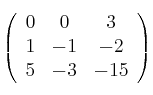Portada del sitio > Fundamentos de Matemáticas > Aplicaciones Lineales y Matrices
Aplicaciones Lineales y Matrices
Todos los Ejercicios del Tema
Artículos de esta sección
-
Dada la aplicación linealSolución
![f:R_2[x]\rightarrow R_3[x] f:R_2[x]\rightarrow R_3[x]](local/cache-TeX/85dc57b7b577fa6a1f3478db60c2dbb6.png) cuya expresión es
cuya expresión es 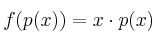 , encuentre la matriz asociada para bases respectivas
, encuentre la matriz asociada para bases respectivas 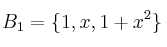 y
y 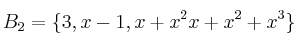 e indique también una base para el subespacio
e indique también una base para el subespacio 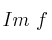
-
Supongamos la matrizSolución
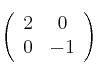 , según las propiedades de las matrices semejantes, ¿qué podría decir del determinante de una matriz semejante a ella?
, según las propiedades de las matrices semejantes, ¿qué podría decir del determinante de una matriz semejante a ella? - Solución
-
Suponiendo una matrizSolución
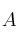 cuadrada regular y de ese mismo orden la matriz cuadrada
cuadrada regular y de ese mismo orden la matriz cuadrada 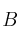 indique la propiedad que cumplen los valores propios del producto de ambas
indique la propiedad que cumplen los valores propios del producto de ambas 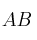 y
y 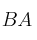
- Solución
- Solución
- Solución