Aplicaciones Lineales y Matrices
Todos los Ejercicios del Tema
Artículos de esta sección
-
Supongamos la matriz
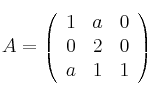
calcule el valor de A para que sea diagonalizable
-
Calcule el siguiente determinante:
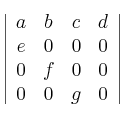
-
Calcule el siguiente determinante:
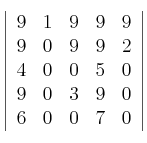
-
Dada la matriz
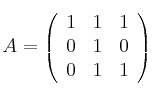
y considerando
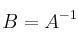
y
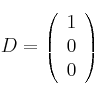
, determine:
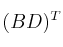
-
Determine los valores de
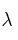
para que la forma cuadrática
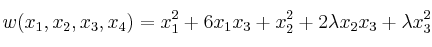
sea definida positiva
-
Dados los números reales no nulos a,b,c y d, deterine el rango de la matriz
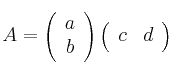
-
Dada una matriz
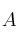
, que hemos introducido en el programa MAXIMA, se ha producido la siguiente salida al escribir la orden
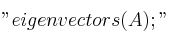
:
![[ [ [ -2,4 ] , [ 2,1 ] ] , [ [ [ 1,0,-1 ] , [ 0,1,0 ] ] , [ [ 1,1,0 ] ] ] ] [ [ [ -2,4 ] , [ 2,1 ] ] , [ [ [ 1,0,-1 ] , [ 0,1,0 ] ] , [ [ 1,1,0 ] ] ] ]](local/cache-TeX/d660119704a58b422aa974bae1d57c4e.png)
Explique su significado
-
Dada la aplicación
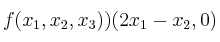
, calcula la dimensión de los subespacios núcleo e imagen
-
Calcule núcleo e imagen de la aplicación lineal de
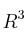
en
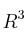
dada por:
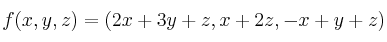
-
Calcule la inversa de la matriz
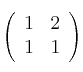
YouTube Twitter

