Portada del sitio > Fundamentos de Matemáticas > Aplicaciones Lineales y Matrices
Aplicaciones Lineales y Matrices
Todos los Ejercicios del Tema
Artículos de esta sección
- Solución
- Solución
- Solución
- Solución
- Solución
-
Dada la forma bilinealSolución
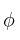 en el cuerpo
en el cuerpo 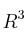 , cuya expresión es:
, cuya expresión es:
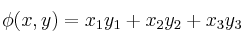 , donde
, donde 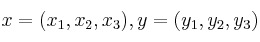 están referidos a la base cacónica de
están referidos a la base cacónica de 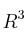 :
:
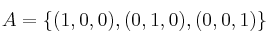 .
¿Cuál sería la matriz asociada a la nueva base
.
¿Cuál sería la matriz asociada a la nueva base 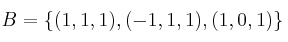 ?
? -
Dada la aplicación T deSolución
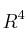 en
en 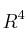 , determinada por la expresión:
, determinada por la expresión:
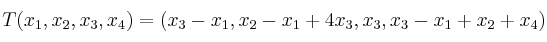 ,
¿cuál es el determinante de su matriz asociada?
,
¿cuál es el determinante de su matriz asociada? -
Sea la matrizSolución
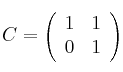 y el conjunto de matrices cuadradas de orden 2x2
y el conjunto de matrices cuadradas de orden 2x2
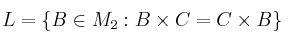 Compruebe si la suma y el producto usuales de matrices son conmutativas en el conjunto L
Compruebe si la suma y el producto usuales de matrices son conmutativas en el conjunto L - Solución

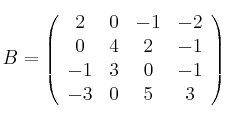
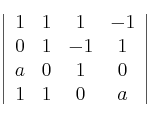 tome valor máximo
tome valor máximo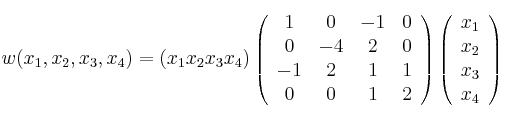 determine las ecuaciones implícitas del subespacio asociado al vector
determine las ecuaciones implícitas del subespacio asociado al vector 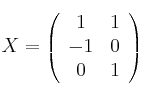 y
y 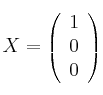 y suponiendo la matriz
y suponiendo la matriz
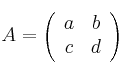 tiene determinante
tiene determinante