23-Probabilidad
Artículos de esta sección
-
Solución
La probabilidad de un suceso
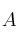 es
es 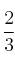 , la de un suceso
, la de un suceso 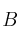 es
es 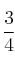 y la de la intersección es
y la de la intersección es 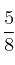 . Calcula de forma razonada la probabilidad de que:
. Calcula de forma razonada la probabilidad de que: a) Se verifique alguno de los sucesos
a) Se verifique alguno de los sucesos
 b) No se verifique ni A ni B
b) No se verifique ni A ni B
 c) Ocurra A si se ha verificado B
c) Ocurra A si se ha verificado B -
Solución
En una determinada ciudad, aparte de su propia lengua, el
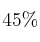 de los habitantes hablan inglés, el
de los habitantes hablan inglés, el 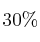 francés, y el
francés, y el 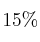 inglés y francés. Calcula la probabilidad de que:
inglés y francés. Calcula la probabilidad de que: a) Un habitante elegido al azar de entre los que hablan francés, hable también inglés.
a) Un habitante elegido al azar de entre los que hablan francés, hable también inglés.
 b) Un habitante de esta ciudad elegido al azar no hable ni inglés ni francés.
b) Un habitante de esta ciudad elegido al azar no hable ni inglés ni francés. -
Solución
En un colegio hay 120 alumnos que cursan el bachillerato, 80 de ellos son de primero. Del total hay 64 chicas y 45 son chicas de primero. Elegimos un alumno al azar, se pide de forma razonada:
 a) ¿Cuál es la probabilidad de que el alumno elegido sea chico de segundo?.
a) ¿Cuál es la probabilidad de que el alumno elegido sea chico de segundo?.
 b) Si el alumno elegido se sabe que es de primero, ¿cuál es la probabilidad de que sea chica
b) Si el alumno elegido se sabe que es de primero, ¿cuál es la probabilidad de que sea chica -
Solución
Se lanzan 3 monedas, la primera de 50 céntimos, la segunda de 1 euro y la tercera de 2 euros. Se consideran los sucesos: Suceso A aparecen dos caras, suceso B aparece una cara en la moneda de 2 euros y el suceso C aparecen caras en las monedas de 50 céntimos y de un euro. Se pide de forma razonada:
 a)
a) 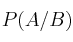
 b) ¿Son independientes los sucesos B y C?
b) ¿Son independientes los sucesos B y C? -
Solución
Una cadena metálica está compuesta por 4 eslabones. La probabilidad de rotura de cada eslabón a un peso de 100 kilos es
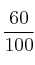 . Se somete la cadena a un peso de 100 kilos, se pide de forma razonada:
. Se somete la cadena a un peso de 100 kilos, se pide de forma razonada: a) La probabilidad de que no se rompa la cadena
a) La probabilidad de que no se rompa la cadena
 b) Si se quiere que la probabilidad de que no se rompa la cadena sea
b) Si se quiere que la probabilidad de que no se rompa la cadena sea 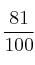 , ?cuál debe ser la probabilidad de rotura de cada eslabón?
, ?cuál debe ser la probabilidad de rotura de cada eslabón? -
Solución
Un jugador profesional lanza un dado trucado. La probabilidad de cada una de las seis caras es:
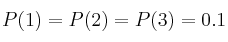 ,
, 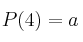 ,
, 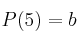 ,
, 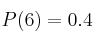 .
.
Sabiendo que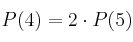 :
: a) Calcula el valor de
a) Calcula el valor de 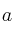 y
y 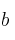
 b) ¿Qué cara debe pedir el jugador para ganar la partida?
b) ¿Qué cara debe pedir el jugador para ganar la partida? -
Una urna, A, contiene 4 bolas rojas, 3 verdes y 2 negras. Otra urna, B, contiene 1 bola roja, 3 verdes y 2 negra. Se saca, al azar, una bola de cada urna y se anota el color. a) ¿Cuál es la probabilidad de que las dos bolas sean negras? b) ¿Cuál es la probabilidad de que las dos bolas sean del mismo color?Solución


