Geometría en el espacio (IV-Pos. Relativas)
Todos los Ejercicios del Tema
Artículos de esta sección
-
Halla la posición relativa de las rectas:
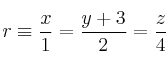
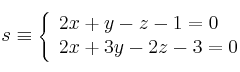
-
Halla la posición relativa de las rectas:
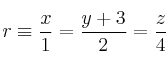
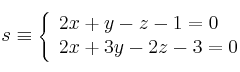
-
Estudia la posición relativa de las rectas:
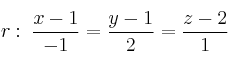
y
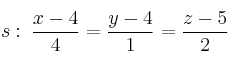
-
Estudia la posición relativa (y punto de corte en caso de ser secantes) de las rectas:
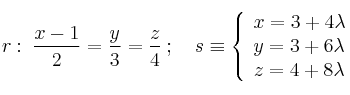
-
Estudia la posición relativa (y punto de corte en caso de ser secantes) de las rectas:
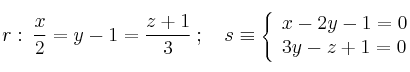
-
Halla el valor de 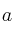 para que se corten las rectas:
para que se corten las rectas:
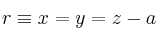
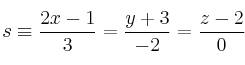
-
Halla la posición relativa (y punto de corte si existe) de las rectas:
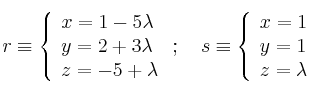
-
Halla la posición relativa (y punto de corte si existe) de las rectas:
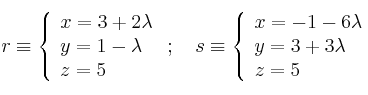
-
Halla la posición relativa de recta y plano:
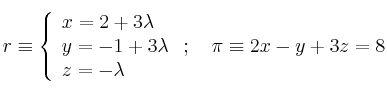
-
Halla la posición relativa de recta y plano:
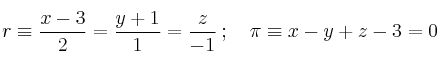
YouTube Twitter

