Geometría en el Espacio (I - Vectores)
Todos los Ejercicios del Tema
Artículos de esta sección
-
Halla el valor de
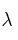
para que los siguientes vectores sean linealmente dependientes:
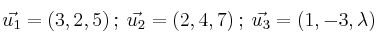
-
Expresa el vector
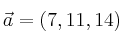
en combinación lineal de los vectores:
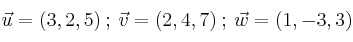
-
-
Dados los vectores
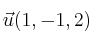
y
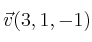
, halla el conjunto de vectores
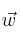
perpendiculares a
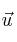
y coplanarios a
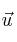
y
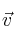
-
Halla el valor de
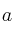
para que los siguientes vectores sean linealmente dependientes:
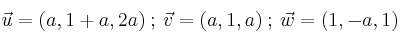
-
Para
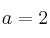
, expresa el vector
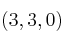
en combinación lineal de los vectores:
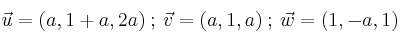
-
Dados los vectores:
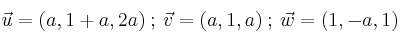
Si sabemos que son linealmente dependientes para
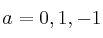
, justifica, de forma razonada y sin desarrollar, que el producto mixto de los vectores
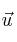
,
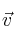
y
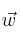
vale 0
-
Halla un vector
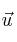
que sea paralelo al vector
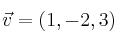
y que determine junto al vector
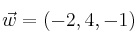
un paraleogramo de 25 unidades cuadradas
-
Halla un vector
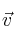
que sea coplanario a los vectorres
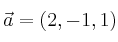
y
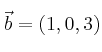
, y además que sea ortogonal al vector
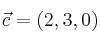
-
Halla el valor de
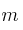
para que los vectores
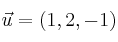
,
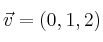
y
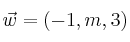
sean linealmente dependientes. Expresa la relación de dependencia.
YouTube Twitter

