Geometría en el Espacio (I - Vectores)
Todos los Ejercicios del Tema
Artículos de esta sección
-
Comprueba que los siguientes vectores forman una base:
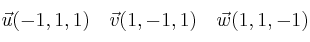
-
Comprueba que los siguientes vectores forman una base:
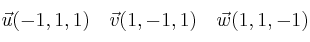
-
Comprueba que los siguientes vectores forman una base:
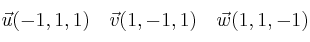
-
Dados los vectores
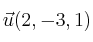
y
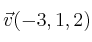
, calcula el producto vectorial
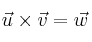
y comprueba que
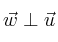
y
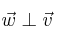
-
Halla el valor de
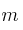
para que los vectores
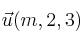
y
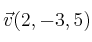
sean ortogonales
-
Halla el ángulo que forman los vectores
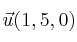
y
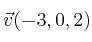
-
Calcula el área del triángulo de vértices
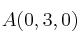
,
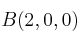
y
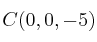
-
Calcula el volumen del paralelepípedo definido por los puntos
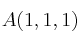
,
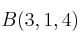
,
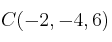
y
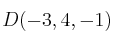
-
Demuestra que los vectores
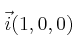
,
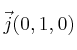
,
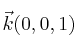
forman una base ortonormal
-
Halla las coordenadas del vector
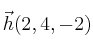
respecto de la base formada por los vectores
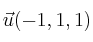
,
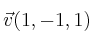
y
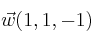
YouTube Twitter

