Portada del sitio > MAT - 2º BACHILLERATO > Programación Lineal
Programación Lineal
Todos los Ejercicios del Tema
Artículos de esta sección
-
Se desea invertir una cantidad de dinero menor o igual que 125000 euros, distribuidos entre acciones del tipo A y del tipo B. Las acciones del tipo A garantizan una ganancia del
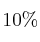 anual, siendo obligatorio invertir en ellas un mínimo de 30000 euros y un máximo de 81000 euros. Las acciones del tipo B garantizan una ganancia de
anual, siendo obligatorio invertir en ellas un mínimo de 30000 euros y un máximo de 81000 euros. Las acciones del tipo B garantizan una ganancia de 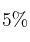 anual, siendo obligatorio invertir en ellas un mínimo de 25000 euros. La cantidad invertida en acciones del tipo B no puede superar el triple de la cantidad invertida en acciones del tipo A. ¿Cuál debe ser la distribución de la inversión para maximizar la ganancia anual? Determínese dicha ganancia máxima.
anual, siendo obligatorio invertir en ellas un mínimo de 25000 euros. La cantidad invertida en acciones del tipo B no puede superar el triple de la cantidad invertida en acciones del tipo A. ¿Cuál debe ser la distribución de la inversión para maximizar la ganancia anual? Determínese dicha ganancia máxima. -
Se desea invertir una cantidad de dinero menor o igual que 125000 euros, distribuidos entre acciones del tipo A y del tipo B. Las acciones del tipo A garantizan una ganancia del
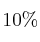 anual, siendo obligatorio invertir en ellas un mínimo de 30000 euros y un máximo de 81000 euros. Las acciones del tipo B garantizan una ganancia de
anual, siendo obligatorio invertir en ellas un mínimo de 30000 euros y un máximo de 81000 euros. Las acciones del tipo B garantizan una ganancia de 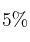 anual, siendo obligatorio invertir en ellas un mínimo de 25000 euros. La cantidad invertida en acciones del tipo B no puede superar el triple de la cantidad invertida en acciones del tipo A. ¿Cuál debe ser la distribución de la inversión para maximizar la ganancia anual? Determínese dicha ganancia máxima.
anual, siendo obligatorio invertir en ellas un mínimo de 25000 euros. La cantidad invertida en acciones del tipo B no puede superar el triple de la cantidad invertida en acciones del tipo A. ¿Cuál debe ser la distribución de la inversión para maximizar la ganancia anual? Determínese dicha ganancia máxima. -
Se desea invertir una cantidad de dinero menor o igual que 125000 euros, distribuidos entre acciones del tipo A y del tipo B. Las acciones del tipo A garantizan una ganancia del
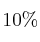 anual, siendo obligatorio invertir en ellas un mínimo de 30000 euros y un máximo de 81000 euros. Las acciones del tipo B garantizan una ganancia de
anual, siendo obligatorio invertir en ellas un mínimo de 30000 euros y un máximo de 81000 euros. Las acciones del tipo B garantizan una ganancia de 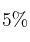 anual, siendo obligatorio invertir en ellas un mínimo de 25000 euros. La cantidad invertida en acciones del tipo B no puede superar el triple de la cantidad invertida en acciones del tipo A. ¿Cuál debe ser la distribución de la inversión para maximizar la ganancia anual? Determínese dicha ganancia máxima.
anual, siendo obligatorio invertir en ellas un mínimo de 25000 euros. La cantidad invertida en acciones del tipo B no puede superar el triple de la cantidad invertida en acciones del tipo A. ¿Cuál debe ser la distribución de la inversión para maximizar la ganancia anual? Determínese dicha ganancia máxima. -
Un distribuidor de aceite de oliva compra la materia prima a dos almazaras, A y B. Las almazaras A y B venden el aceite a 2000 y 3000 euros por tonelada, respectivamente. Cada almazara le vende un mínimo de 2 toneladas y un máximo de 7 y para atender a su demanda, el distribuidor debe comprar en total un mínimo de 6 toneladas. El distribuidor debe comprar como máximo a la almazara A el doble de aceite que a la almazara B. ¿Qué cantidad de aceite debe comprar el distribuidor a cada una de las almazaras para obtener el mínimo coste? Determínese dicho coste mínimo.
-
Una empresa de fabricación de ventanas tiene dos fábricas en las ciudades A y B, con una capacidad de producción de 800 y 1200 ventanas respectivamente. Han de transportar ventanas a 3 obras situadas en e localidades distintas. La primera obra necesita 1000 ventanas, la segunda 700 y la tercera 600. Si los costes de envío de cada ventana son los que aparecen en la siguiente tabla, organiza los envíos para que el coste sea mínimo.
Obra 1 Obra 2 Obra 3 Fábrica A 3 7 1 Fábrica B 2 2 6 -
Una empresa láctea se plantea la producción de dos nuevas bebidas A y B. Producir un litro de la bebida A cuesta 2€, mientras que producir un litro de bebida B cuesta 0,5€. Para realizar el lanzamiento comercial se necesitan al menos 6 millones de litros de bebida, aunque del tipo B no podrán producirse (por limitaciones técnicas) más de 5 millones y debido al coste de producción no es posible elaborar más de 8 millones de litros en total de ambas bebidas. Además, se desea producir una cantidad de bebida B mayor o igual que la de bebida A. ¿Cuántos litros habrá que producir de cada tipo de bebida para que el coste de producción sea mínimo? Calcúlese dicho coste. Justifíquense las respuestas.


