16-Funciones
Artículos de esta sección
-
La temperatura T, en grados, que adquiere una pieza sometida a un proceso viene dada en función del tiempo t, en horas, por la expresión:
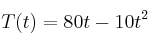 siendo
siendo 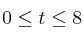
 a) Representar gráficamente la función.
a) Representar gráficamente la función.
 b) Determinar cuando alcanza la temperatura máxima la pieza y el valor de ésta.
b) Determinar cuando alcanza la temperatura máxima la pieza y el valor de ésta.
 c) ¿Qué temperatura tendrá la pieza al cabo de una hora?
c) ¿Qué temperatura tendrá la pieza al cabo de una hora?
 d) ¿Cuando alcanzará la pieza una temperatura de
d) ¿Cuando alcanzará la pieza una temperatura de  ?
? -
La temperatura T, en grados, que adquiere una pieza sometida a un proceso viene dada en función del tiempo t, en horas, por la expresión:
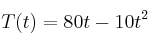 siendo
siendo 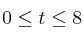
 a) Representar gráficamente la función.
a) Representar gráficamente la función.
 b) Determinar cuando alcanza la temperatura máxima la pieza y el valor de ésta.
b) Determinar cuando alcanza la temperatura máxima la pieza y el valor de ésta.
 c) ¿Qué temperatura tendrá la pieza al cabo de una hora?
c) ¿Qué temperatura tendrá la pieza al cabo de una hora?
 d) ¿Cuando alcanzará la pieza una temperatura de
d) ¿Cuando alcanzará la pieza una temperatura de  ?
? -
La temperatura T, en grados, que adquiere una pieza sometida a un proceso viene dada en función del tiempo t, en horas, por la expresión:
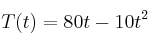 siendo
siendo 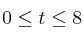
 a) Representar gráficamente la función.
a) Representar gráficamente la función.
 b) Determinar cuando alcanza la temperatura máxima la pieza y el valor de ésta.
b) Determinar cuando alcanza la temperatura máxima la pieza y el valor de ésta.
 c) ¿Qué temperatura tendrá la pieza al cabo de una hora?
c) ¿Qué temperatura tendrá la pieza al cabo de una hora?
 d) ¿Cuando alcanzará la pieza una temperatura de
d) ¿Cuando alcanzará la pieza una temperatura de  ?
? -
[2]Para la siguiente función dibuje su gráfica, calcule dominio y rango. Estudie un punto donde la función sea continua y otro donde sea discontinua:
![f(x) =
\left\{
\begin{array}{lrc}
- \frac{\sqrt{4-(x+3)^2}}{2} - 1 & si & x < 1
\\-x^2+2x-1 & si & -1 \leq x < 1
\\ 2 - |x-2| & si & 1 < x \leq 4
\\ 8-2x & si & 4 < x < 6 \\
\left[ x+2 \right] -1 & si & x > 6
\end{array}
\right. f(x) =
\left\{
\begin{array}{lrc}
- \frac{\sqrt{4-(x+3)^2}}{2} - 1 & si & x < 1
\\-x^2+2x-1 & si & -1 \leq x < 1
\\ 2 - |x-2| & si & 1 < x \leq 4
\\ 8-2x & si & 4 < x < 6 \\
\left[ x+2 \right] -1 & si & x > 6
\end{array}
\right.](local/cache-TeX/bddcf52e4b1421ae27f82e5d0336c861.png)
-
[4]Para la siguiente función dibuje su gráfica, calcule dominio y rango. Estudie un punto donde la función sea continua y otro donde sea discontinua:
![f(x) =
\left\{
\begin{array}{lrc}
- \frac{\sqrt{4-(x+3)^2}}{2} - 1 & si & x < 1
\\-x^2+2x-1 & si & -1 \leq x < 1
\\ 2 - |x-2| & si & 1 < x \leq 4
\\ 8-2x & si & 4 < x < 6 \\
\left[ x+2 \right] -1 & si & x > 6
\end{array}
\right. f(x) =
\left\{
\begin{array}{lrc}
- \frac{\sqrt{4-(x+3)^2}}{2} - 1 & si & x < 1
\\-x^2+2x-1 & si & -1 \leq x < 1
\\ 2 - |x-2| & si & 1 < x \leq 4
\\ 8-2x & si & 4 < x < 6 \\
\left[ x+2 \right] -1 & si & x > 6
\end{array}
\right.](local/cache-TeX/bddcf52e4b1421ae27f82e5d0336c861.png)

![y = \frac{x}{[1-x]+2} + 2\sqrt{3x-x^2} + \frac{x^2+x+1}{|x^2-4|} y = \frac{x}{[1-x]+2} + 2\sqrt{3x-x^2} + \frac{x^2+x+1}{|x^2-4|}](local/cache-TeX/61dee14210ae1614b569dadc92fe570c.png)