
	INICIO Clientes \| Blog MATEMÁTICAS \| QUÍMICA \| FÍSICA \| Matemát. UNIVERSIDAD \| ALEMÁN

Portada del sitio > MAT - 1º BACHILLERATO > 24-Distribución Binomial

24-Distribución Binomial

Todos los Ejercicios del Tema

Artículos de esta sección

Disponemos de una caja con bombillas (algunas de ellas defectuosas). Elegimos 2 bombillas al azar. Consideremos la variable aleatoria "Número de bombillas defectuosas". Se pide:

Espacio Muestral
Justificar que es una variable aleatoria discreta
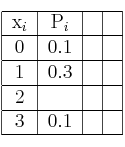
Tabla de distribución de probabilidad
Comprobar que la suma de todas las probabilidades vale 1
Disponemos de una diana con 6 círculos concéntricos numerados del 1 al 6. Obtenemos la siguiente tabla de distribución de probabilidad:

$\begin{tabular}{|l|c|c|c|c|c|c|}\hline x_i & 1 & 2 & 3 & 4 & 5 & 6\\ \hline P_i & 0,32 & 0,28 & a & 0,12 & 0,06 & 0,01\\ \hline \end{tabular}$

Halla el valor de $a$ y de las siguientes probabilidades:

$P(X \geq 4)$
$P(X < 3)$
$P(2 < X < 4)$
$P(X < 4)$
Lanzamos 3 monedas. Consideremos la variable aleatoria "Número de caras obtenidas". Se pide:

Espacio Muestral
Justificar que es una variable aleatoria discreta
Tabla de distribución de probabilidad
Media (esperanza matemática) y desviación típica
Completa la siguiente tabla de distribución de probabilidad de una variable aleatoria discreta y calcula los parámetros (media y desviación típica).

$\begin{tabular}{|c|c|c|c|}\hline x_i & P_i & & \\ \hline 0 & 0.1 & & \\ \hline 1 & 0.3 & & \\ \hline 2 & & & \\ \hline 3 & 0.1 & & \\ \hline \end{tabular}$
Extraemos dos cartas (sin reemplazamiento) de una baraja española y consideramos la variable aleatoria "Número de Ases obtenidos". Calcula media y desviación típica.
Extraemos una ficha de un juego de dominó y consideramos la variable aleatoria que anota la "Suma de Puntos obtenidos". Calcula media y desviación típica.
Hemos estudiado 12 de los 30 temas de un examen. Se eligen, al azar, 2 de los 30 temas. Consideremos la variable aleatoria que anota el número de temas que conocemos. Describe su tabla de distribución de probabilidades.
Disponemos de una urna con 3 bolas Rojas, 5 Blancas y 2 Verdes. Extraemos dos bolas y consideramos la variable aleatoria "Número de bolas rojas obtenidas". Se pide: Tabla de distribución de probabilidad en los casos:

a) Sin Reemplazamiento
b) Con Reemplazamiento
Consideremos una variable aleatoria $X$ que sigue una distribución binomial $B(7, 0.4)$ . Calcula:

a) $P[X=2]$
b) $P[X=5]$
c) $P[X=0]$
d) $P[X>0]$
e) $P[X>3]$
f) $P[X \leq 3]$
Consideremos una variable aleatoria $X$ que sigue una distribución binomial $B(9, 0.2)$ . Calcula:

$P[X < 3]$
$P[X \geq 3]$
$P[X \neq 0]$
$P[X \geq 1]$
$P[X \leq 9]$