Portada del sitio > Ejercicios de EXAMEN > Mat. Básicas
Acceso Universidad Mayores 25 - Mat. Básicas
Ejercicios de EXAMEN
Ejercicios de EXAMEN
funciones
Teoría
Artículos
-
3020 - 5_UNED_2008_S_I
El límite de
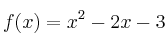 cuando
cuando 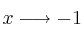 es:
es: a) 0
a) 0
 b) -4
b) -4
 c) 2
c) 2 -
3025 - 10_UNED_2008_S_I
Para
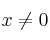 , la función
, la función 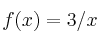 tiene derivada
tiene derivada a)
a) 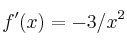
 b)
b) 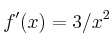
 c)
c) 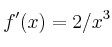
-
3028 - 4_UNED_2008_S_B
La función
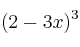 tiene derivada:
tiene derivada: a)
a) 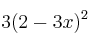
 b)
b) 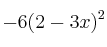
 c)
c) 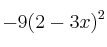
-
3032 - 7_UNED_2008_S_B
El límite de
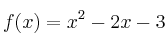 cuando
cuando 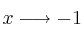 es:
es: a) 0
a) 0
 b) 2
b) 2
 c) -4
c) -4 -
3067 - 5_UNED_2008_J_A
La función
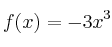 tiene derivada
tiene derivada a)
a) 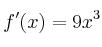
 a)
a) 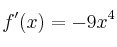
 a)
a) 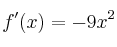
-
3070 - 8_UNED_2008_J_A
El gráfico de la función
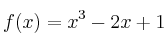 no pasa por el punto
no pasa por el punto a)
a) 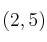
 b)
b) 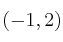
 c)
c) 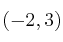
-
3071 - 9_UNED_2008_J_A
El punto
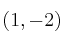 pertenece a la recta:
pertenece a la recta: a)
a) 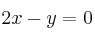
 b)
b) 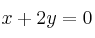
 c)
c) 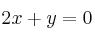
-
3074 - 3_UNED_2008_J_H
La función
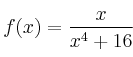
 a) es continua en todos los puntos
a) es continua en todos los puntos
 b) es discontinua en
b) es discontinua en 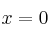
 c) es discontinua en
c) es discontinua en 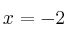
-
3078 - 8_UNED_2008_J_H
La derivada de
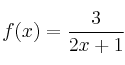 en el punto
en el punto 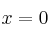 vale:
vale: a) -6
a) -6
 b) -3
b) -3
 c) -2
c) -2 -
3081 - 4_UNED_2007_S_C
La expresión
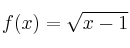 define una función
define una función 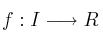 si
si a)
a) 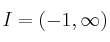
 b)
b) 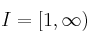
 c)
c)