Cantabria Mayo 2012

Artículos de esta sección

• 

   

  Una editorial va a editar tres libros A, B y C con un coste por unidad de 6, 8 y 10 euros respectivamente. El importe total de la edición es de 14.500 euros. Sabemos que

   si al número de ejemplares de B le sumamos el doble del número de ejemplares de C se obtiene el número de ejemplares de A.

   el número de ejemplares de A es igual a m veces el número de ejemplares de B. Se pide:

   a) Plantear un sistema de ecuaciones que permita calcular cuántos libros de cada tipo se van a editar.
   b) Determinar para que valores del parámetro real m el sistema tiene solución.
   c) Resolver el sistema para m=5 .

• 

   

  Considere la función 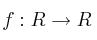definida por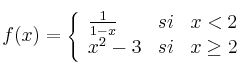

   Determine el dominio de definición de la función f y estudie su continuidad.
   Calcule las asíntotas de la función f y los puntos de corte con los ejes. Esboce la gráfica de la función f .
   Calcule el área del recinto limitado por la gráfica de la función, el eje OX (recta y=0) y las rectas x=2 y x=4 .

• 

   

  Considere los puntos A = ( 1 , 2 , 3 ) , B = ( -1 , 0 , 2 ) y C = ( 2 , -1 , 0 )

   a) Calcule la ecuación general del plano 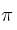que contiene a A ,B y C
   b) Determine el área del triángulo de vértices A , B y C .
   c) Halle la ecuación de la recta r que es perpendicular al plano 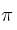y pasa por el punto P ( 1 , 1 , 1 )

• 

   

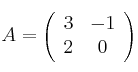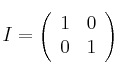  Considere las matrices: , y

  a) Determine para qué valores del parámetro k la matriz B tiene inversa

  b) Para k = 4 , calcule la matriz inversa de B

  c) Para k = 4 , determine la matriz C que verifica